Uma
relação R
sobre um
conjunto S
é chamado de ordem de S
se R
é reflexiva, antissimétrica e transitiva. Um conjunto S
munido de uma relação de ordem parcial R
é dito um conjunto parcialmente ordenado.
Exemplo:
a) A relação 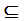 de
uma inclusão conjuntista é uma ordem parcial sobre qualquer coleção
de conjuntos, uma vez que a inclusão conjuntista tem as três
propriedades desejadas.
de
uma inclusão conjuntista é uma ordem parcial sobre qualquer coleção
de conjuntos, uma vez que a inclusão conjuntista tem as três
propriedades desejadas.
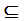 de
uma inclusão conjuntista é uma ordem parcial sobre qualquer coleção
de conjuntos, uma vez que a inclusão conjuntista tem as três
propriedades desejadas.
de
uma inclusão conjuntista é uma ordem parcial sobre qualquer coleção
de conjuntos, uma vez que a inclusão conjuntista tem as três
propriedades desejadas.
b) A
relação <= sobre o conjunto R
dos números reais é reflexiva, assimétrica e transitiva. Assim <= é uma ordem parcial em R.
c) A
relação “a divide b” (a\b)é uma ordem parcial sobre o
conjunto N
dos números inteiros positivos. Contudo “a divide b” não é
uma ordem parcial sobre o conjunto Z
dos inteiros, uma vez que a/b e b/a não implica a=b. Exemplo: 3/-3
e -3/3, mas 3 ≠ -3.
Referência bibliográfica:
LIPSCHUTZ, Seymour; LIPSON, Marc. Matemática discreta. 3. ed. Porto Alegre: Bookman, 2013. xi, 471p. (Coleção Schaum). ISBN 9788565837736.




Nenhum comentário:
Postar um comentário