Estamos muito acostumados a utilizar as relações em nosso cotidiano, tais como "maior que", "menor que", entre outras. Essas relações são responsáveis pela existência ou inexistência de conexão entre pares de objetos.
Seguindo a definição, o termo relação deve significar relação binária.
 |
| Imagem ilustrativa, não refere-se ao exemplo abaixo. Wikipédia. |
Como um exemplo de relação, temos que A=(1,2,3) e B={x,y,z}, sendo R={(1,y),(1,z),(3,y)}.
-R é uma relação de A em B, sendo R um subconjunto de AxB.
-O domínio de R é {1,3} e a imagem é {y,z}.
Relação inversa:
Utilizando o mesmo exemplo citado acima, podemos determinar a inversa de R, denotada por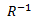 . Fazendo a inversa da função R={(1,y),(1,z),(3,y)}, temos como resultado:
. Fazendo a inversa da função R={(1,y),(1,z),(3,y)}, temos como resultado:
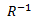 . Fazendo a inversa da função R={(1,y),(1,z),(3,y)}, temos como resultado:
. Fazendo a inversa da função R={(1,y),(1,z),(3,y)}, temos como resultado:
O domínio e a imagem de 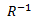 são iguais ao domínio e imagem de R, pois se R é qualquer relação, então (R^-1)^-1=R.
são iguais ao domínio e imagem de R, pois se R é qualquer relação, então (R^-1)^-1=R.
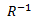 são iguais ao domínio e imagem de R, pois se R é qualquer relação, então (R^-1)^-1=R.
são iguais ao domínio e imagem de R, pois se R é qualquer relação, então (R^-1)^-1=R.
Referência bibliográfica:
LIPSCHUTZ, Seymour; LIPSON, Marc. Matemática discreta. 3. ed. Porto Alegre: Bookman, 2013. xi, 471p. (Coleção Schaum). ISBN 9788565837736.